Issue 23	Winter 1998

Social Research Update is published quarterly by the Department of Sociology, University of Surrey, Guildford GU2 7XH, England. Subscriptions for the hardcopy version are free to researchers with addresses in the UK. Apply by email to sru@soc.surrey.ac.uk.

Multilevel Models

Ian Plewis is a Senior Lecturer in Statistics at the Institute of Education, University of London and a member of the Multilevel Models Project team. He is also Senior Research Officer at the Thomas Coram Research Unit, Institute of Education. He has research interests in the design and analysis of longitudinal studies, multilevel modelling of categorical data, and in the determinants of young children’s educational progress. He acknowledges the support from Phase Two of the ESRC programme on the Analysis of Large and Complex Datasets for the production of this review.

• Multilevel modelling extends more traditional statistical techniques by explicitly modelling social context. This introduces a degree of realism often absent from single-level models such as multiple regression.
• Many of the populations of interest to social scientists have a hierarchical, or nested structure. Some have a cross-classified structure. Multilevel models analyze the levels of these structures simultaneously. Consequently, questions about the appropriate level of analysis are redundant.
• Multilevel modelling techniques can fruitfully be applied to repeated measures data and to multivariate data, and are especially valuable in these situations when data are missing.
• A range of software enables multilevel models to be fitted easily.

Many social scientists aim to explain variability in human behaviour and attitudes, and how these behaviours are modified and constrained by shared membership of social contexts -- the family, the school, the workplace and so on. One way in which social scientists further their understanding of social behaviour is by using statistical models to analyze quantitative data. A weakness of the way in which these models are often applied to social data is that they focus too much on the individual, and too little on the social and institutional contexts in which individuals are located. Multilevel modelling aims to redress the balance, by emphasizing both individuals and their social contexts.

Population Structure

Commonly, populations of interest to social scientists have a hierarchical or nested structure. To give two examples, individuals live in households which, in turn, are located in geographically defined communities. And pupils are taught in classes within schools within Local Education Authorities. Hierarchically structured populations can be thought of as pyramids with different numbers of levels. In the first example, there are three levels: individuals as the base level or level one, households as an intermediate level (level two) and communities as the highest level or apex, level three. In the second example, there are four levels: pupils, classes, schools and LEAs. In a nested structure, each individual belongs to just one household, each pupil to just one class, and so on up the hierarchy. In principle, there is no limit to the number of levels of a hierarchy but, in practice, we are rarely in the position to carry out analyses with more than four levels of nesting.

Most of the developments in multilevel modelling up to now have been concerned with analyzing data with a nested structure. However, some populations have a cross-classified structure. For example, patients can be defined by their family doctor and by the hospital they attend. However, GPs can refer their patients to a number of different hospitals, and hospitals draw their patients from a number of GPs, and so GPs and hospitals form a cross-classification within which patients are nested.

Extending Multiple Regression

The aim of most statistical models is to account for variation in a response variable by a set of one or more explanatory variables. The actual model used will be influenced by a number of considerations, foremost being the nature of the response -- whether it is binary, categorical or continuous. Multilevel modelling techniques have been developed for each of these cases, but we will confine ourselves here to continuously measured responses, those situations where multiple regression methods have traditionally been used.

Let us build up the ideas by way of a simple example. Suppose a researcher is interested in the relation between educational attainment at age 16 (the response) and household income (the explanatory variable), for all pupils in England. Suppose a large sample is selected which has been clustered by secondary school. Hence, we have just two levels -- pupil and school.

A traditional regression model is specified as:

ATTAINMENT = a + b INCOME + e_i    (1)

with e_i the residual term for pupil i, and interest is in the size of b, the effect of income on attainment. In models of this kind, the coefficients a and b are often called ‘fixed’ effects.

This model does not, however, recognize that pupils are taught in schools. Hence, the specification is incomplete and potentially misleading because the institutional context is missing. For example, it is possible that mean attainment varies from school to school, after allowing for the effect of income on attainment. One implication of this is that pupils’ attainments within schools are more alike, on average, than attainments in different schools, and this might lead to some interesting findings about the effect of schools. One penalty for ignoring the effect of school in model 1 is that the standard error of the regression coefficient, b, is too low. Essentially the same problem arises in survey research if we base our estimates of precision on the assumption of simple random sampling, rather than accounting for the clustered nature of our sample.

We should therefore extend model 1 to:

ATTAINMENT = a_j + b INCOME + e_ij    (2)

We now have two subscripts, one for each of the two levels -- i for pupils and j for schools. Also, we have a_j rather than just a to represent the variability in the intercept from school to school. This can be referred to as the ‘school effect’, which we treat as a ‘random’ effect and which we represent as a variance. Consequently, we now have a multilevel model; in fact, a simple two-level model which is sometimes known as a variance components model.

The distinction between fixed and random effects is an important one in multilevel modelling. We could represent the effect of school on attainment in model 2 as a set of dummy variables, the size of this set being one less than the number of schools. If we have a study with just a few schools, this would be a reasonable approach. If, however, we have a sample with many schools, estimating so many fixed effects (a₁, a₂ etc.) is inefficient. It is much more efficient just to estimate a single variance, the variance between the schools’ intercepts.

Random Slopes

The simple two-level model -- model 2 -- allows the intercept to vary from school to school. We might also like the slope, b, to vary from school to school, because schools might influence the relation of income to attainment, with some schools reinforcing it and others reducing it. Hence, we can write:

ATTAINMENT = a_j + b_j INCOME + e_ij    (3)

and we now have two random effects -- a_j as before and now b_j to represent the variability in slopes from school to school. We must also allow the schools’ intercepts and slopes to be correlated. This more complicated model is sometimes called a random slopes, or a random coefficients model.

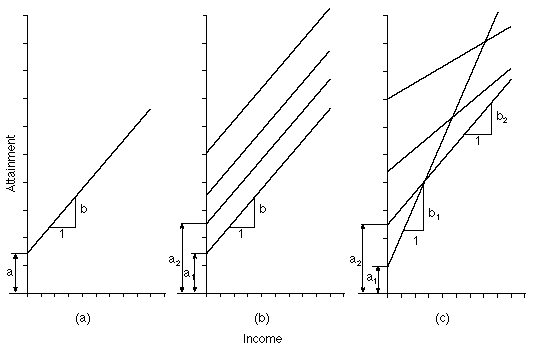
Figure 1: Models of increasing complexity

The three panels of Figure 1 show how we have introduced complexity into our model, and hence made it more realistic. Panel (a) illustrates the simple regression model, model 1. In panel (b), the intercepts are allowed to vary but the slopes are constant (model 2). In panel (c), corresponding to model 3, both the intercepts and slopes vary from school to school, and, in this particular case, there is a negative correlation between intercept and slope. In panels (b) and (c) we have included just four out of many schools for illustration.

We can now extend the distinction between fixed and random effects with another example. Suppose a researcher is interested in the effects of income on an attitude for two kinds of social contexts -- living in different geographically defined communities and belonging to a particular social class. Community is a random effect; we sample from the population of communities and we are interested in saying something about communities in general, rather than about one particular community. This kind of social context -- the effect of community -- can be represented by two kinds of random effects, by the variance between communities in mean attitude (analogous to Figure 1b), and by the variance between communities in the relation, or slope, between income and attitude (analogous to Figure 1c). However, social class is a fixed effect; we are interested in the effects of each class and it does not make sense to sample from a ‘population’ of social classes. We introduce this kind of social context by estimating the size of the statistical interaction between income and social class on attitude, thus allowing for the possibility that the relation between income and attitude varies across social classes. These interaction terms are also fixed effects.

An Illustration

Suppose we have estimated the random slopes model (model 3) on a large sample, both of pupils (5000, say) and, importantly, of schools (200, say). Our response is a score generated from pupils’ GCSE results. Suppose the between school, or level-two variance in the intercept is 4, and the between school variance in the slopes is 0.04. This implies that, at mean income, about 95% of the schools’ intercepts lie within 4 units of the mean intercept (i.e within two standard deviations, twice the square root of 4), and about 95% of the school slopes lie within 0.4 units of the mean slope (twice the square root of 0.04). Finally, if the variance of the pupil residual, eij, is 8 then, at mean income, one third of the total variation in GCSE results is between schools (4/(4+8)) and two thirds within schools. We can see, from Figure 1c, that between school variation varies by income in a random slopes model.

Using multilevel modelling techniques with these data gives us more information about the relation between attainment and income than we would have had if we had used a single-level model. (It is, of course, possible, that the school random effects turn out to be small. In these cases, which only become apparent after the event, a single-level model is sufficient.) On the other hand, results such as these are tantalizing because they give no indication why, for example, the relation between attainment and income varies as much as it does from school to school. One possibility is that variables measured at the school level account for some of the between school variation. For example, suppose we can divide the sample schools into two groups -- those which use some form of selection at age 11 and those which do not. Our multilevel model can be extended to incorporate these ‘school-level’ variables, which vary from school to school but not from pupil to pupil within a school.

The existence of variables measured at different levels sometimes leads researchers to ask ‘at which level should I analyze my data?’. A strength of the multilevel approach is that it renders such questions redundant. Data can, and should, be collected and analyzed at all levels simultaneously. This avoids the pitfalls associated with aggregation. Suppose, for example, we only had measures of school mean attainment and school mean household income, and we fitted a simple regression to these aggregated data. We would typically find that the relation between attainment and income is much stronger at the school level than it is, on average, at the pupil level. This is often referred to as the ecological fallacy. Attainment and income are, however, individual-level (or level-one) variables, and should be measured and modelled at that level, within a multilevel model which allows for institutional effects.

Other Extensions

There are two other situations for which a multilevel approach is particularly useful. The first is with repeated measures data. Suppose we have a sample of individuals whose income is measured annually over a number of years. We can think of this as a nested structure with the occasions of measurement defining level one and the individuals defining level two. (Not all multilevel structures have individuals at the lowest level.) We can now model income as a smooth function of time, and see how, and why, the parameters of this function vary from individual to individual. It is not necessary for each individual to have the same number of measurements, and so the approach can encompass missing data. Multivariate data can also be modelled as multilevel data. Then, the different variables measured for each individual define level one, with the individuals themselves defining level two. And if these individuals are, in turn, members of different social or geographical groups, then we can discover whether the structure of associations between the variables is different at different levels.

Conclusion

Multilevel modelling techniques offer quantitative social researchers the opportunity not only to analyze their data in a technically more appropriate way than traditional single-level methods do, but also to extend the kinds of questions they can ask of their data, and hence the opportunity to model contextual richness and complexity. But like all statistical techniques, they cannot replace social theory (although the results might add to it), interpretation is usually more of a challenge than computation, and they must be used with due attention paid to their assumptions. We do require, however, reasonably large numbers of higher-level units to carry out satisfactory analyses.

Software and Resources

There are two main specialist packages for multilevel modelling. These are MLwiN, produced by the Multilevel Models Project at the Institute of Education, University of London with ESRC support, and, from the United States, HLM (HLM stands for Hierarchical Linear Modelling). Both operate in a Windows environment. In addition, some multilevel modelling is possible within major statistical packages such as SAS (PROC MIXED). Rapid developments in statistical computing, and methodological advances in modelling mean that further software developments are likely.

In addition, there is an electronic multilevel discussion list, which can be joined by sending a message ‘join multilevel firstname lastname’ to mailbase@mailbase.ac.uk. There is also a Multilevel Models Newsletter, published twice yearly with ESRC support by the Multilevel Models Project (e-mail m.yang@ioe.ac.uk). Further details about MLwiN can be found on the Project web site (http://www.ioe.ac.uk/mlwin/) and general information about multilevel modelling at http://www.ioe.ac.uk/multilevel/.

Bibliography

Social Research Update is published by:

Edited by Nigel Gilbert.

Winter 1998 © University of Surrey

Permission is granted to reproduce this issue of Social Research Update provided that no charge is made other than for the cost of reproduction and this panel acknowledging copyright is included with all copies.