Issue 32	Spring 2001

Social Research Update is published quarterly by the Department of Sociology, University of Surrey, Guildford GU7 5XH, England. Subscriptions for the hardcopy version are free to researchers with addresses in the UK. Apply to SRU subscriptions at the address above, or email sru@soc.surrey.ac.uk.

A PDF version of this article is available here.

Soft Modelling the Predictors of Drug Treatment Use

R. Frank Falk, Ph.D. is a professor of sociology at the University of Akron in Akron, Ohio, USA. In 2000 he was an International Visiting Fellow in Social Research Methods at the University of Surrey. His areas of interest include structural equation modeling, computer assisted analysis of qualitative data, and adult emotional development. He is currently developing a coding system for the analysis of biographical data. Dr. Falk has given numerous presentations, conducted workshops, and published a book and several articles on latent variable path analysis with partial least squares.

Peggy Tonkin, Ph. D. is a research associate at the University of Akron Institute for Health and Social Policy. Her areas of research include substance abuse prevention and treatment, and the sociology of education.

• Soft Modelling creates optimal linear relationships among constructs specified by a conceptual model.
• Manifest (observed) variables in soft modelling may be measured at nominal, ordinal, or interval levels; and models may include variables measured at different levels.
• Spurious relationships, common in complex models with many variables, are easily identified with soft modelling procedures.
• Soft Modelling is useful in quasi-experimental designs and observational studies with either very small or very large sample sizes.

This paper explains soft modelling and illustrates the technique with an example from a study of the predictors of alcohol and drug treatment use. The four points above represent some of the strengths of soft modelling for data analysis in non-experimental research.

Soft modelling is a form of structural equation modelling that imposes few assumptions about the level of measurement, the sample size, or the scope of the theory. In relaxing these assumptions, one can argue for neither a confirmatory conclusion nor a probability index of overall model fit. Instead, the researcher is able to see how measurements fit together to form a construct with the use of principal components. Estimates of the multiple R squared are given for the predictive relationship between components. These results are based on a conceptual model that the researcher must specify in advance. We were interested in the effects of enrolment in a government disability program and the availability of medical insurance on the number of times respondents reported involvement in some type of drug or alcohol treatment program over the course of a two year study period. The respondents were followed over a two-year period to evaluate the impact of a policy change that eliminated the disability classification for drug and alcohol addiction. The subjects in this sample were dropped from the supplemental income program and had the option of reapplying under some other disability or losing their cash and medical insurance benefits. Samples were drawn from nine city or county areas in five of the continental United States beginning in December, 1996. Our baseline measurements were taken immediately preceding the official cut-off date of January 1, 1997 and every six months after, for a total of five interview waves. Nine hundred and fifty seven subjects had complete data across all five of the data points.

Our conceptual model is presented in Figure 1. We were interested in predicting treatment use across the four interview waves after the baseline from data on the severity of problems experienced in several life domains: the respondent’s perceived need for drug or alcohol treatment; the type (modality) of treatment, if any, in which the respondent was involved at baseline; high risk drug behaviours; and the respondent’s medical insurance and disability income status after baseline.

Manifest variables that measure each construct are grouped together. A principal components analysis assigns a weight to each manifest variable and the weighted variables are added together to give a score for each construct. The constructs are then correlated, and a path analysis is computed. This is a conceptual presentation of the mathematics of soft modelling; the actual computation is more complex (Falk & Miller, 1992, Lomoeller, 1989, Wold 1980). The computer program we use for soft-modelling is Latent Variable Path Analysis with Partial Least Squares Estimation (Lomoeller, 1988) and is available from Dr. Jack McArdle at the University of Virginia (http://krypton.psyc.virginia.edu/jack.mcardle).

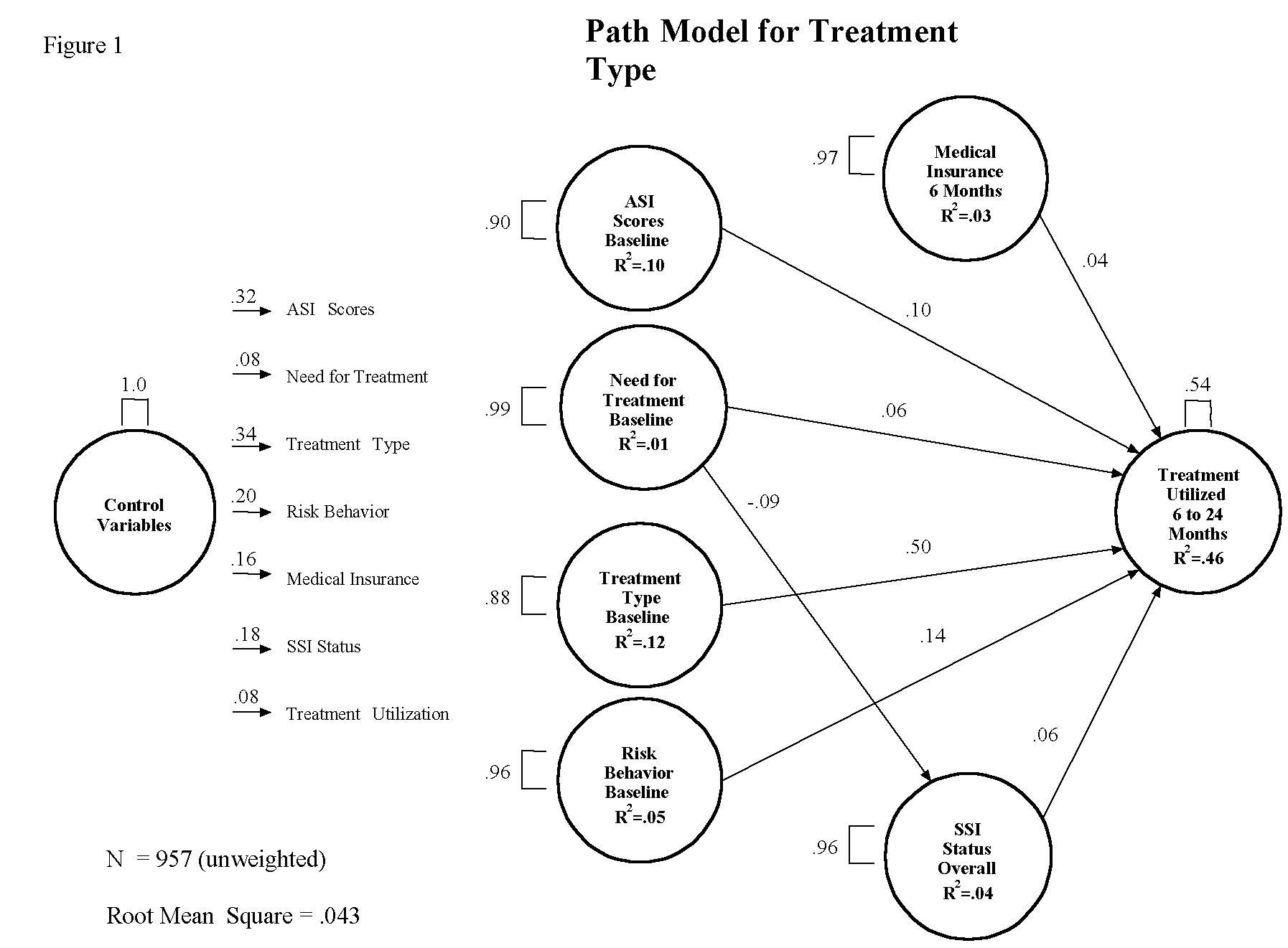
Figure 1 illustrates the proposed relationships (14 paths in all) between our eight constructs. The proposed relationships in the model come from the general literature on treatment entry and retention and the expected effects of the policy change. Preliminary analyses revealed significant differences between sample locations on treatment use; therefore, site was entered as a control variable and allowed to predict each of the other seven constructs. The paths from the demographic control construct are shortened to provide ease in reading. Our conceptual model follows the control construct in temporal order: addiction severity index scores, the need for treatment, treatment type at baseline, risk behaviours, medical insurance and disability income status are each allowed to predict treatment use. The need for treatment is allowed to predict disability income status.

Before we consider each of the hypothesised relationships between these constructs, we should be satisfied with the reliability of our measurements. Sixteen variables were measured as indicants of the eight constructs. The indicants included nominal, interval, and ratio levels of measurement. They included measurements from well-established instruments such as the Addiction Severity Index Scores (see McLelland, Luborsky, Cacciola, and Griffith 1984). For a complete description of the study, see Tonkin, Swartz, and Kappagoda, forthcoming.

In our study, most of the measurements proved to be reliable (see Table 1). Principal component loadings above 0.55 are generally desirable. However, several observed variables with very small loadings were left in the model because our goal was to examine the comparative effects of each of the predictors. Low loadings indicated that the variables are not contributing substantially to the construct and thus are not good measures of the proposed construct. For example, the loading of 0.05 for involvement in a jail or prison treatment program at baseline indicates this variable is not a substantial contributor to the treatment type construct. Conversely, participation in methadone maintenance at baseline is the defining measure for the baseline treatment modality construct with a loading of 0.98.

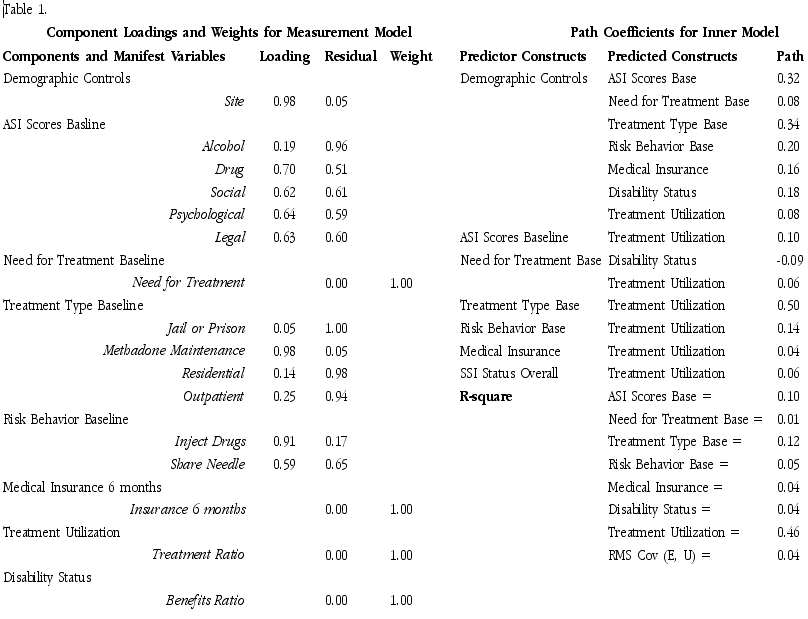
Researchers, in general, should expect principal component loadings to be above 0.55 before examining the relationships between the theoretical constructs. Generally, three or more manifest variables are preferred as multiple indicants of a construct. When there is only one indicant for each construct, the programme becomes a standard path analysis procedure.

As we stated in the beginning, soft modelling creates optimal linear relationships among constructs specified by a conceptual model. It does this by an iterative process in which each predictor construct is made to be as good a predictor as it can be, while the predicted construct is made to be the best predicted construct it can be. To achieve this optimisation, the principle component loadings on the manifest variables are adjusted. This is accomplished in two stages by using the least squares minimisation procedure within each group of manifest variables and their construct and then between the constructs. This optimisation procedure provides the researcher with three important pieces of information: the matrix of correlations between the constructs, the path coefficients between the constructs as specified in the model, and the multiple R square value for each predicted construct. With this information, we are able to evaluate our original conceptual model.

The correlation matrix allows us to assess if the relationships are going in the predicted direction. In our model, we assumed that all the proposed relationships would be in a positive direction. The path coefficients give the direct effects and direction of relationship between the predictor construct and the predicted construct. These are the equivalent of standardised regression coefficients or beta weights, and so may be directly compare with one another. They differ from the correlation coefficients because they take into account the correlations between the predictor constructs.

The multiple R square is the measure of the total amount of variance in the predicted construct that is accounted for by the predictor constructs. These provide an estimate of the effect of all the predictors taken together on the predicted construct. Traditional statistical tests of significance can be applied to the multiple R square.

With these three pieces of information, we can evaluate how well our model predicts the relationships in our original conceptualisations. The results noted in Table 1 provide the information necessary to evaluate our conceptual model. The first piece of information to evaluate is whether the multiple R square is high enough to believe that our predicted constructs are in fact being predicted by their predictor constructs. In this case, only three of the seven constructs had statistically significant multiple R squares and our model predicted 10, 12, and 46 percent of the variance in the predicted constructs. Next we examine the contribution of each predictor construct to the multiple R squared, the contribution of each is referred to as the percent of variance contributed. It is approximated by multiplying the path coefficient by the correlation coefficient. When this value is less than 0.015 or less than 1.5 %, the predictor construct is not making an important contribution to the variance in the predicted construct and the path should be eliminated (Falk & Miller, 1992). In this example, the paths from medical insurance and disability income status should be dropped from the model because both the correlation values and the path values are small. The path from need for treatment to overall disability income status should also be dropped. However, they are left in the model because they are the constructs of most interest in this study. The path from need for treatment to treatment use is small, but the correlation coefficient between the two constructs is large. The product of the two is greater than 0.015; therefore, the path is left in the model.

Once all unimportant paths have been eliminated, the remaining path coefficients should be compared to their respective correlation coefficients for any suppressor effects. If the signs of the two coefficients do not agree, a suppressor effect is present. Models with many correlated variables are likely to have suppressors. However, these effects may not be true suppressor effects, but mathematical artefacts. The easiest way to determine which type of effect is present is to compare the multiple R squares before and after eliminating the suspect path. If the multiple R square does not change significantly after removing the path, the suppressor is an artefact and the path should be removed.

Worth noting is that much of the variance in our model is accounted for by differences among the nine sample sites. This is apparent from the relatively large path coefficients emanating from the demographic control construct. The construct for the Addiction Severity Index scores had a positive impact on treatment use as was hypothesised. The size of the impact was small but its relative size makes it one of the best predictors of treatment use in the model. By far the best predictor of treatment use is the type of treatment in which the subject participated at baseline. Since methadone maintenance defines this construct, the large path coefficient indicates that respondents who were in methadone maintenance at baseline were very likely to be in treatment at later points in the study. The need for treatment at baseline, medical insurance, and disability income status are the weakest predictors of treatment use. Only the path from need for treatment to disability income status produced a sign contrary to our predicted direction. Since the sign of the path coefficient matches the direction of the correlation coefficient, the observed relationship is in fact a negative one and not the result of a suppressor effect. The negative path indicates subjects who felt they needed treatment at baseline were less likely to be receiving disability income benefits after baseline.

A snapshot of our findings reveals that a statistically significant amount of variation was accounted for in three of our predicted constructs. Forty-six percent of the variation in treatment use after baseline is accounted for by the seven predictor constructs, with methadone maintenance accounting for more than half of the 46 percent. Less than five percent of the variance in each of the two main predictors of treatment use (medical insurance and disability income status) is accounted for by the four preceding predictors. The demographic control construct (sample site) is the best predictor of both these constructs. What the findings suggest is that controlling for site differences, treatment use at an earlier point in time is the best predictor of treatment at a later point in time. Specifically, involvement in a methadone maintenance program at baseline is the best predictor of treatment use over the course of the study.

References

Social Research Update is published by:

Edited by Nigel Gilbert.

Spring 2001 © University of Surrey

Permission is granted to reproduce this issue of Social Research Update provided that no charge is made other than for the cost of reproduction and this panel acknowledging copyright is included with all copies.