Social Research update logo
Issue 30 Autumn 2000

Social Research Update is published quarterly by the Department of Sociology, University of Surrey, Guildford GU7 5XH, England. Subscriptions for the hardcopy version are free to researchers with addresses in the UK. Apply to SRU subscriptions at the address above, or email sru@soc.surrey.ac.uk.

Adobe PDF logo A PDF version of this article is available here.

A re-examination of segregation indices in terms of compositional invariance

Chris Taylor, Stephen Gorard and John Fitz

Chris Taylor is a research associate working on an ESRC-funded study of the social composition of schools at the School of Social Sciences, Cardiff University. Stephen Gorard and John Fitz are both Readers at the School of Social Sciences working on the same project. The team have recently published ‘Questioning the crisis account: a review of evidence for increasing polarisation in schools’ in Educational Research (2000) 42, 3.

Measurement of social segregation by organisational unit is as dependent on the method used as on the data being analysed. In a sense, the same dataset can lead to different conclusions depending on the index of segregation employed. Therefore, given the range of methods available, it is important for the researcher to decide first on a definition of segregation (stratification, polarisation, or association), and only then to select an appropriate index. Perhaps the most commonly used method has been the Dissimilarity Index (D), since it is arguably unaffected by simple changes in population composition while remaining sensitive to changes in population distribution. However, this paper argues that D is affected by scaling of the numerator, and cannot therefore be considered fully composition invariant. Since this previously unreported characteristic is yet another factor to consider in the selection of an appropriate tool for each task, we propose an alternative which is closely related but overcomes this potential problem.

The role and validity of various indices of segregation have been a focus of considerable debate and speculation over the last fifty years in social science research, and have therefore been the subject of several previous issues of Social Research Update (e.g. Blackburn and Jarman 1997, Gorard 1999). Similar debates have occurred in many fields including the analysis of: residential patterns by ethnicity; gendered patterns of occupation; polarised income patterns in family economics, and the social composition of schools in education. During these years it is possible to distinguish at least two ‘index wars’. The first of these apparently crowned the Dissimilarity Index as the premier of all measures (Peach 1975). The more recent war seems to have moved the focus of attention away from individual measures of segregation, towards a consideration of composite measures, which identify different elements of segregation (Massey et al. 1996). Despite this shift in the epistemological debate the prevalence of particular indices has remained relatively unchanged since the first index war, 1947-55.

Dissimilarity and other indices

The Dissimilarity Index (D), or index of dissimilarity or displacement index as it has been variously named, has been used consistently since a paper by Duncan & Duncan (1955a). This presented a number of segregation indices and showed that they were all related to the segregation or Lorenz curve and, hence, to each other. However, it was another article by the same authors (1955b), which made explicit use of the Dissimilarity Index for their own research, that may have proved the catalyst for the current extensive use of D as a measure of segregation (see Lieberson 1981). The standard formula for D is given below, and although there have been other representations of the formula (see for example Massey & Denton 1988 and Waslander & Thrupp 1995) all are consistent with the one presented in Duncan & Duncan (1955a).

For any area with sub-areas in which segregation may take place, the index of dissimilarity may be defined as:

D = 0.5 × Sum |Ai /X - Bi /Y|
Using gender segregation by occupation as an example: Ai and Bi are the number of mutually exclusive cases in occupation i, giving a total of Ci cases in occupation i, X is the sum of Ai where i varies from 1 to n (the number of occupations), Y is the equivalent sum for Bi, and Z is the equivalent sum for Ci (see Table 1).

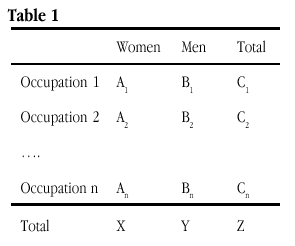
Table 1

One basis for the repeated use of D in segregation research, despite criticism (e.g. by Blackburn and Jarman 1997), has been the way that it appears to meet the key criteria as generally agreed for an index of segregation. James & Taeuber (1985), for example, suggested that there were four such criteria for indices to satisfy:
Size invariance -The index should be unaffected by the size of the area(s) used for analysis. For example, the same picture should emerge nationally and locally.

Organisational equivalence -The index should be unaffected by changes in the number of sub-areas, by combination for example of two sub-areas on the same ‘side’ of the line of no segregation.

Principle of transfers -The index should be capable of being affected by the movement of one individual from sub-area to sub-area.

Composition invariance -The index should be unaffected by scaling of columns or rows, through increases in the ‘raw’ figures which leave the proportions otherwise unchanged.

Watts (1998) argued that for any analysis of segregation over time both composition invariance and occupation invariance are key to our understanding of a useful measure. These were defined in the following way -‘Compositional invariance refers to the invariance of the index, following uniform changes in the number of males and females in each occupation reflecting the overall, but typically unequal, percentage changes in male and female employment [...] Occupations invariance requires that the measure of segregation be invariant to changes in the relative size of occupations if the gender composition of these occupations remains constant’ (1998:490). These two criteria would ensure that the measure of segregation would not be affected by either an increase in the absolute levels of a particular group across all sub-areas, or an increase in the absolute levels of all groups in a particular sub-area (such that the relative composition of each sub-area remained unaltered)

It is criteria like these, which we would support, that have led to the decline of other previously suggested measures of segregation, inequality or polarisation such as the Variance ratio, Information theory index, index of Isolation, and the Atkinson index, and to the pre-eminence of D. The Dissimilarity Index, unlike many of the ‘losers’ in the war, has long been considered as composition invariant, for even though Duncan & Duncan acknowledge that the proportion of both subgroups is present in the calculation they argue that D is unaffected by changes in either group. For example, Lieberson (1981) claims that D is not affected by population composition, and gives as an example ‘if the number of whites in each subarea was divided by ten, then the index of dissimiliarity would remain unchanged’ (p.63). One of the primary purposes of this paper is to argue that on a strong interpretation of composition invariance this is not, in fact, so (or that at least D does not meet both of the requirements as described by Watts above).

Table 2 presents a hypothetical example of the number of students in four schools who are eligible for free school meals (FSM is an indicator of families defined as in poverty). D for this set of schools is 0.267. The fourth column shows what proportion of the total number of children in poverty are in each school. The final column shows what proportion of the total number of children in each school are in poverty

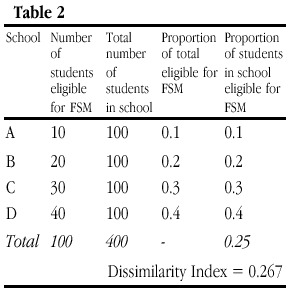
Table 2

Obviously, in the trivial case where all of the numbers in Table 2 are scaled (so that School A takes 20 FSM students from a total of 200 for example), D remains the same. Additionally, as Lieberson and others have pointed out, if the number of students eligible for free school meals is doubled in each school, perhaps reflecting a period of economic recession, then D remains the same (Table 3). This is so despite changes in the proportion of students in poverty in each schools (column 5) since the proportion in each school of the total in poverty remains the same as in Table 2 (column 4). However, it should be noted that this invariance only applies if the number of students not eligible for free school meals is held constant (and this proviso is seldom acknowledged in verbal descriptions of the index properties). This is what we term here ‘weak’ composition invariance.

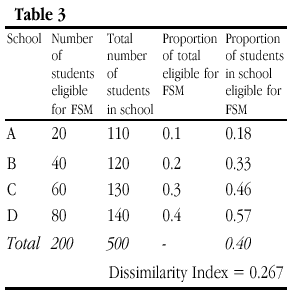
Table 3

If, instead, the number of students in poverty rises as a proportion of an existing school population but in such a way that the relative distribution of students in poverty remains unchanged between schools, then D varies. In Table 4, D increases to 0.4, which suggests that segregation has increased even though the proportion of the total students eligible for free school meals is the same for each school as it was in Tables 2 and 3. Put simply, a doubling of the figures for column 5 leads to an increase in D, yet it is far from clear that the schools in Table 4 are any more segregated (i.e. with FSM more unevenly distributed between schools) than those above. What D is picking up here is simply an increase in poverty across all schools.

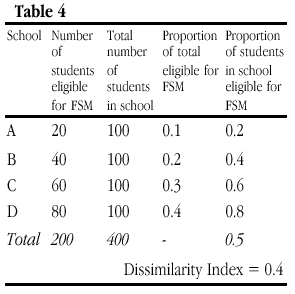
Table 4

These three hypothetical examples illustrate one potential misinterpretation of figures of segregation whether in school intakes, as represented here, or in ethnicity of cities or the gendered division of labour, in situations with differing composition. To be ‘strongly’ composition invariant an index must be unaffected by changes in the relative frequency of the groups being measured. As an example, an occupation containing 20% of the total workforce but only 10% of the women in the workforce cannot be said to be more or less segregated simply because the overall number of women in the workforce changes, but only if the 10% and 20% figures change. The point is similar in many respects to that made about achievement gaps in Gorard (1999). Simple scaling of the numerator should not lead to changes in either achievement gaps or measures of segregation. Yet this apparently simple rule leads to paradox whereby either the figures in Table 3 or the figures in Table 3 are seen as differently segregated to those of Table 2.

The Segregation Index

An alternative measure of segregation, the Segregation index (S) proposed by Gorard (2000), does have strong composition invariance (and unlike the Matching Marginals, or the calculation of Yule’s Q and related methods such as odds ratios, is not restricted to consideration of 2¥2 tables). Whether the relative size of one sub-group is changed, or if two or more sub-groups are equally altered S remains the same. The calculation of S is similar to that of the Hoover coefficient for income inequality (Kluge 1998), and uses the difference between the proportion of a particular group in a single sub-area and the proportion of all group members in the same sub-area. Using the same terms as above:

S = 0.5 × Sum|Ai /X -Ci /Z|

This is similar in many respects to D, having mostly the same properties and leading to comparable results in many real-life situations. For example, Table 5 shows both indices used to analyse the distribution of eligibility for free school meals in secondary schools in Swansea from 1990 to 1997. While both indices give different actual figures these are, in a sense, arbitrary. What matters here is that allowing for rounding errors the two figures are in perfect agreement about the rise and fall of segregation between schools in Swansea.

Table 5

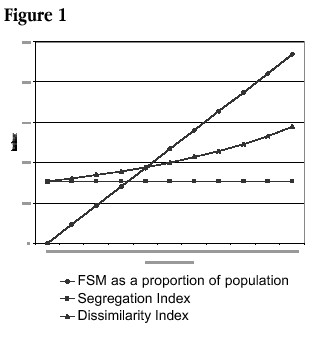
The key difference is in the base figure used to compare the distribution of any particular group. Hence, while D compares the proportion of two groups with each other by sub-area, S compares the proportion of one group with the total for that sub-area. This means that even if the proportion of students eligible for free school meals is altered, S remains unchanged as long as they are distributed to each of the schools in the same proportions as the original figures. This is illustrated in Figure 1 which shows the effects on both indices of artificially changing the overall proportion of students eligible for free school meals across the whole of one local education authority (Camden in 1994), while retaining the initial proportion of students eligible for free school meals in each school. As can be seen, S remains constant irrespective of changes to the absolute levels of students eligible for free school meals. However, the effects of such changes on D are clearly evident and curvilinear.

Figure 1

The relationship between the two indices can be expressed as:
D = S + Sum(Ci /Z -Bi /Y) or D = S×Z/Y

Therefore the dissimilarity index, like the index of isolation and others but unlike the segregation index, is measuring two different components of the composition and distribution of cases. Both S and D change as the proportion of existing FSM is altered between schools, and both also change when the overall proportion of FSM changes and is allocated differentially to schools. However, only D changes when the proportion of FSM changes otherwise.

Conclusion

As noted above, the choice between the segregation index and the index of dissimilarity may make little practical difference in some real-life situations. However, the differences between them are important and worthy of further investigation, particularly in terms of what we have called strong and weak composition invariance. Given that in most social science investigations of segregation the differences between places or over time can be very small, it follows that even small differences between indices can be significant. It is quite clear that any empirical consideration of segregation by area or inequality between groups, however defined, requires analytical tools such as indices to summarise the complex patterns of change over time and place. It is also clear that the choice of an index must be subsidiary to the working definition of inequality to be used in the study, and that one index alone may not be able to encapsulate that definition. For these reasons, more than the technical pros and cons of each index, debates about the use of indices are likely to continue (for example some commentators have suggested that the key question is not, as here, how are the groups distributed but how likely is it that a member of one group ‘meets’ another).

The segregation index proposed here was devised in just such an empirical manner. The original form in which it was published betrays its derivation from a verbal definition of what segregation between sub-areas actually is (see Gorard and Fitz 1998). The original proposal also included another technique, described as the segregation ratio, which combined well with the index in measuring aspects of the process of segregation which the overall index is less sensitive to (for example identifying the sub-areas in which segregation is worst). The chief recommendation for the segregation index is that it is strongly composition invariant, making it particularly appropriate for a study of changes in FSM over time since while poverty has increased dramatically over the last ten years the school population has not. The segregation index is the only index we have encountered which is thus able to separate the overall relative growth of FSM from changes in the distribution of FSM between schools. It is suitably ironic that some commentators in educational research have turned this situation on its head and argued that our index is sensitive to changes in composition, while the decomposed index of isolation (Noden 2000) or even unscaled percentage point differences (Gibson and Asthana 2000) are composition invariant. That is how wars start!

References

Blackburn, R. and Jarman, J. (1997) Occupational gender segregation, Social Research Update, 16

Duncan, O. B. & Duncan, B. (1955a) ‘A methodological analysis of segregation indexes’, American Sociological Review 20:210-217.

Duncan, O. B. & Duncan, B. (1955b) ‘Residential distribution and occupational stratification’, American Journal of Sociology 60(5):493-503.

Gibson, A. and Asthana, S. (2000) ‘What’s in a number?’, Research Papers in Education , 15, 2

Gorard, S. (1999) Examining the paradox of achievement gaps, Social Research Update, 26

Gorard, S. (2000) Education and Social Justice, Cardiff: University of Wales Press

Gorard, S. and Fitz, J. (1998) The more things change.... the missing impact of marketisation, British Journal of Sociology of Education, 19, 3, 365-376

James, D. R. & Taeuber, K. E. (1985) ‘Measures of segregation’. In Tuma, N. (ed) Sociological Methodology. Jossey-Bass, San Francisco, pp.1-32.

Kluge, G. (1998) Wealth and people: Inequality measures, Entropy and Inequality Measures. http://www.ourworld.compuserve.com

Lierberson, S. (1981) ‘An asymmetrical approach to segregation. In Peach, C., Robinson, V. & Smith, S. (eds) Ethnic Segregation In Cities. Croom Helm, London.

Massey, D. S. & Denton, N. A. (1988) ‘The dimensions of residential segregation’, Social Forces 67:373-393.

Massey, D. S., White, M. J. & Phua, V. (1996) ‘The dimensions of segregation revisited’, Sociological Methods & Research 24(2):172-206.

Noden, P. (2000) Rediscovering the impact of marketisation, British Journal of Sociology of Education (forthcoming)

Peach, C. (1975) Urban Social Segregation. Longman, New York.

Waslander, S. & Thrupp, M. (1995) ‘Choice, competition, and segregation’, Journal of Education Policy 10:1-26.

Watts, M. (1998) ‘Occupational gender segregation: Index measurement and econometric modelling’, Demography 35(4):489-496.

Social Research Update is published by:

Department of Sociology
University of Surrey
Guildford GU7 5XH
United Kingdom.

Telephone: +44 (0) 1 483 300800
Fax: +44 (0) 1 483 306290

Edited by Nigel Gilbert.

Autumn 2000 © University of Surrey

Permission is granted to reproduce this issue of Social Research Update provided that no charge is made other than for the cost of reproduction and this panel acknowledging copyright is included with all copies.